Cross-Validation: Model Evaluation and Generalization
What are different types of cross-validation techniques?
Cross-validation is a powerful statistical technique for estimating the performance of a predictive model. However, it’s often misunderstood and misused.
What is Cross-Validation?
At its core, cross-validation involves partitioning the dataset into multiple subsets, training the model on a portion of the data, and then evaluating its performance on the remaining unseen data. This process is repeated multiple times, with each subset serving as both training and testing data. By averaging the performance across these iterations, cross-validation provides a more reliable estimate of a model's performance compared to a single train-test split.
Types of Cross-Validation
K-Fold Cross-Validation:
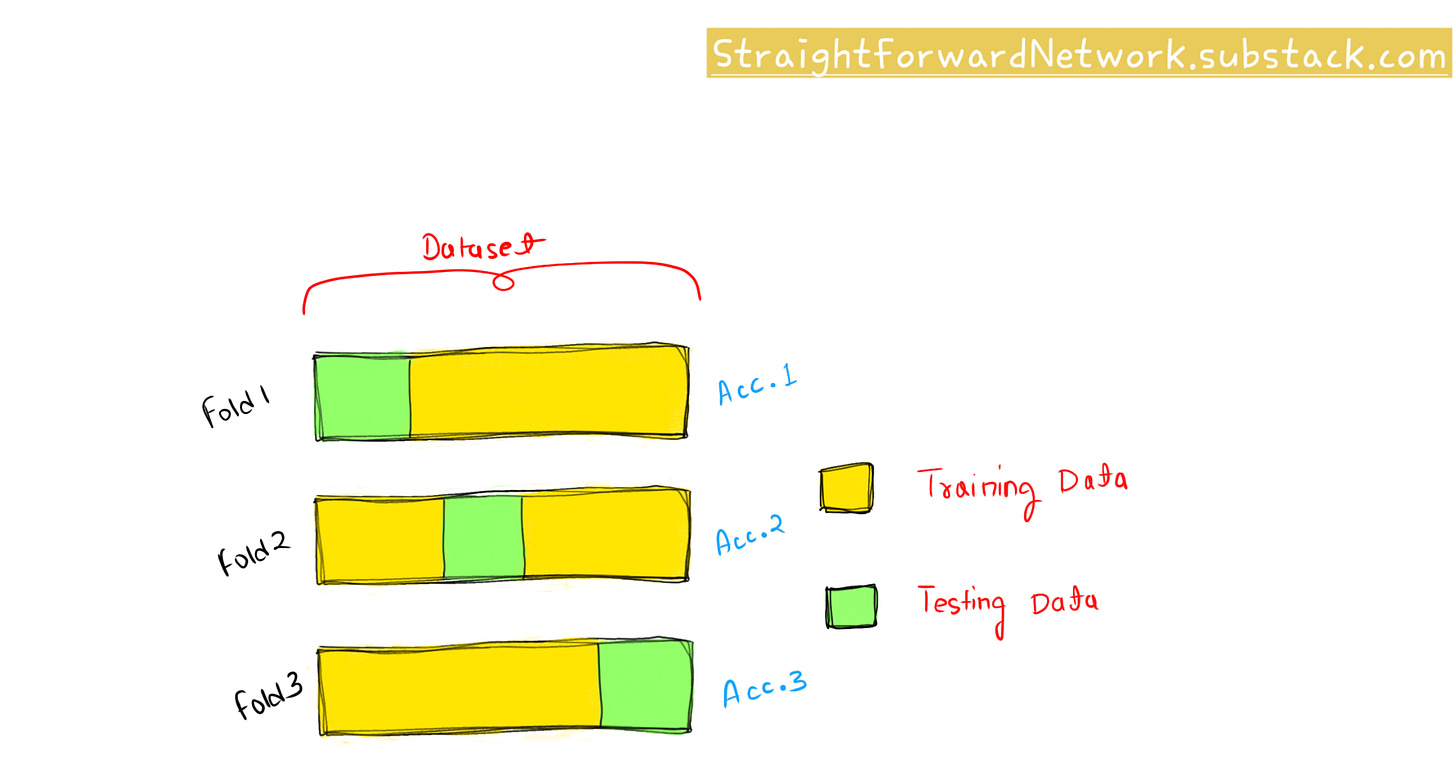
In K-Fold Cross-Validation, the dataset is divided into K equal-sized folds. The model is trained K times, each time using K-1 folds for training and the remaining fold for validation. The final performance metric is the average across all K iterations.
Mathematically, if we denote the performance metric as M and the number of folds as K, the formula for K-Fold Cross-Validation can be represented as:
\({M}_{CV} = \frac{1}{K}{\sum }_{i = 1}^{K}{M}_{i}\)Example: Let's consider a dataset with 100 samples divided into 5 folds. Each fold contains 20 samples. The process involves training the model 5 times, using 4 folds for training and 1 fold for validation in each iteration.
Stratified K-Fold Cross-Validation:
Stratified K-Fold Cross-Validation ensures that each fold maintains the same class distribution as the original dataset. This is particularly useful for imbalanced datasets where certain classes are underrepresented.
Example: If a dataset contains 80% class A and 20% class B, each fold in stratified K-Fold CV will also contain 80% class A and 20% class B.
Leave-One-Out Cross-Validation (LOOCV):
In LOOCV, only one data point is used for validation, and the remaining data points are used for training. This process is repeated for each data point in the dataset.
Mathematically, if we have N data points, the LOOCV involves N iterations.
LOOCV provides a more unbiased estimate of model performance but can be computationally expensive for large datasets.
Common Misconceptions
Misconception 1: Cross-validation is a way to build models
Cross-validation is not a model-building technique but a way to estimate how well a model will perform on unseen data. The actual model building is done using a machine learning algorithm.
Misconception 2: A higher k in k-fold cross-validation leads to a better model
A higher k does not necessarily lead to a better model. It simply means that the original sample is divided into more folds, leading to a slightly less biased estimate of the model skill, but the variance of the estimate may increase.
Incorrect Ways of Using Cross-Validation
Mistake 1: Performing cross-validation after data preprocessing
Cross-validation should be performed before any data preprocessing steps. This is because cross-validation’s purpose is to estimate the performance of the model when it encounters unseen data.
Mistake 2: Using cross-validation as a final model
The results of cross-validation are not a model that we can use to make predictions on new data. Cross-validation is a way to validate the performance of a model, not a model itself.
Correct Usage of Cross-Validation
Step 1: Data Splitting
Split the data into k groups or folds. For example, if we choose k=3, we divide our data into 3 subsets.
Step 2: Model Training and Evaluation
For each unique group:
Take the group as a test data set
Take the remaining groups as a training data set
Fit a model on the training set and evaluate it on the test set
Retain the evaluation score and discard the model
Step 3: Result Aggregation
The result of cross-validation is often given as the mean of the model skill scores, along with the variance or standard deviation.
Conclusion
Cross-validation empowers data scientists to build models that not only perform well on training data but also generalize effectively to unseen data. By understanding the nuances of different cross-validation methodologies, avoiding common pitfalls such as data leakage, and following best practices, we can make more informed decisions about the model's performance.